粒子群最適化
群知能に属するアルゴリズム 粒子群最適化を実装する.
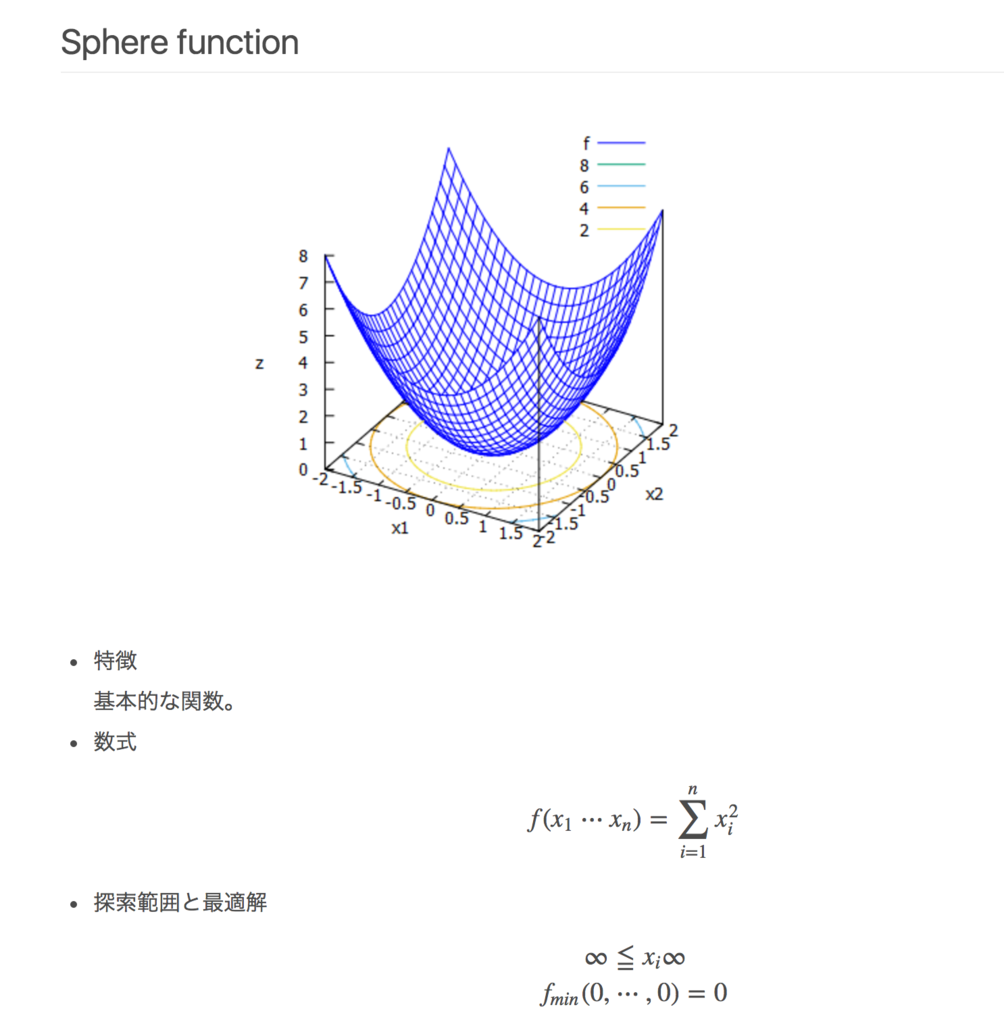

このSphere functionと Rosenbrock functionに粒子群最適化を適用する.
粒子群最適化
これは多次元空間において位置と速度を持つ粒子群でモデル化される。これらの粒子はハイパー空間を飛びまわり、最善な位置を探す。位置の評価は適応度関数で行う。群れのメンバーは良い位置について情報交換し、それに基づいて自身の位置と速度を調整する。このコミュニケーションは主に次の二種類の方法でなされる。
最も良い位置にいる粒子が全体に通知される。
ローカルなベストの位置にいる粒子が近傍の粒子群に通知される。位置と速度の更新は以下の式で行われ、これが繰り返される。
は、慣性定数。多くの場合 1 より若干小さい値が最適である。
と
は群のうちで良い位置に向かう粒子の割合。1 に近い値が多くの場合最適である。
と
は
の範囲の値をとる乱数。
は、その粒子がこれまでに発見したベストな位置
は群全体としてこれまでに発見したベストな位置。これをローカルなベスト
にすれば、上記の後者の方法(近傍への通知)になる。
アルゴリズム
- 各粒子について
と
をランダムに初期化。値の範囲は問題の設定に依存する。
を現在位置に初期化。
を群全体で最も良い適応度を持つ粒子の位置に初期化。
での適応度がしきい値より小さく、かつループ回数が事前に設定した回数に達していないうちは、以下を繰り返し実行する。
- 各粒子について、以下を実行する。
- 上述の式に従って
を更新する。
- 新たな位置での適応度を計算する。
での適応度よりも良い値が得られたら、
を置き換える。
での適応度よりも良い値が得られたら、
を置き換える。
- 上述の式に従って
を更新する。
- 上述の式に従って
- 各粒子について、以下を実行する。

